Hampel Webservice Bottom Content
Dieser Service wird von QuoData kostenlos angeboten. Bitte erwähnen Sie uns in den sozialen Medien, wenn Sie ihn nützlich finden. Und wir freuen uns immer über Ihre Ideen.
Im Gegenzug bitten wir Sie, uns Ihre E-Mail-Adresse zu hinterlassen. Diese wird von uns vertraulich behandelt und nicht an Dritte weitergegeben. Ihre E-Mail-Adresse nutzen wir, um Sie über Neuigkeiten aus den Bereichen Standardisierung, Schulung und Softwareangebote von QuoData auf dem Laufenden zu halten. Sie erhalten weniger als 10 E-Mails pro Jahr.
Q/Hampel als Software mit PROLab implementieren
PROLab ist eine Softwarefamilie zur Planung, Organisation, Durchführung und Analyse von Ringversuchen – also sowohl für Eignungsprüfungen zur Beurteilung der Leistungsfähigkeit von Laboren (typischerweise nach ISO/IEC 13528 und ISO 17043) als auch für Ringversuche zur Validierung analytischer Methoden (typischerweise nach ISO 5725 1-6).
Die Konzeption von PROLab basiert auf den in den einschlägigen internationalen Normen beschriebenen Methoden und auf hochentwickelten mathematisch-statistischen Werkzeugen. Statistische Auswertungen in PROLab werden gemäß den folgenden Rechenstandards durchgeführt:
- ISO 13528/ISO 5725-5 (der sogenannte „A+S-Algorithmus“)
- ISO 5725-2 für Methodenvalidierungsstudien
- DIN 38402 A42
- DIN 38402 A45 (Q/Hampel)
- Schweizer Lebensmittelhandbuch
- Q/Huber-Methode
- Adaptive Horwitz-Funktion
- ISO 5725-3 für verschachtelte PT-Designs
PROLab wird von einigen der wichtigsten PT-Anbieter weltweit verwendet und empfohlen, wie zum Beispiel:
- die US-amerikanische Food and Drug Administration,
- das Gemeinsame Forschungsstelle der Europäischen Kommission,
- die britischen Health and Safety Laboratories und
- das deutsche Bundesamt für Verbraucherschutz und Lebensmittelsicherheit (BVL)
- die Integrierte BioBank Luxemburg (IBBL), die unsere Online-Dateneingabe nutzt Werkzeug.
Es wird auch in unternehmensweiten Qualitätssicherungsprogrammen verwendet, wie beispielsweise bei AngloAmerican
Vergleich von A+S und Q/Hampel
Die Q/Hampel-Methode ist wesentlich robuster als die A+S-Methode. Das bedeutet, dass ihre Ergebnisse bei Ausreißern wesentlich zuverlässiger sind.
Beispiel: Wie Sie in den folgenden beiden Diagrammen sehen können, ergeben beide Methoden sehr ähnliche Mittelwerte und Toleranzgrenzen. Dementsprechend liegen die vier Ausreißer (Labore 33, 37, 27 und 20) außerhalb der von beiden Methoden berechneten Toleranzgrenzen. Beachten Sie, dass im Fall von A+S die vier zuvor bestraften Ausreißer jetzt innerhalb der Toleranzgrenzen liegen. Eine einzige Änderung reicht aus, um die A+S-Berechnungen aus dem Gleichgewicht zu bringen, was zu einer völlig anderen Leistungsbewertung für diese vier Labore führt. Im Fall von Q/Hampel haben sich die Toleranzgrenzen – und der Mittelwert – jedoch kaum verschoben. Die vier zuvor bestraften Labore liegen immer noch außerhalb der Toleranzgrenzen.
Q/Hampel hat sich nicht täuschen lassen:
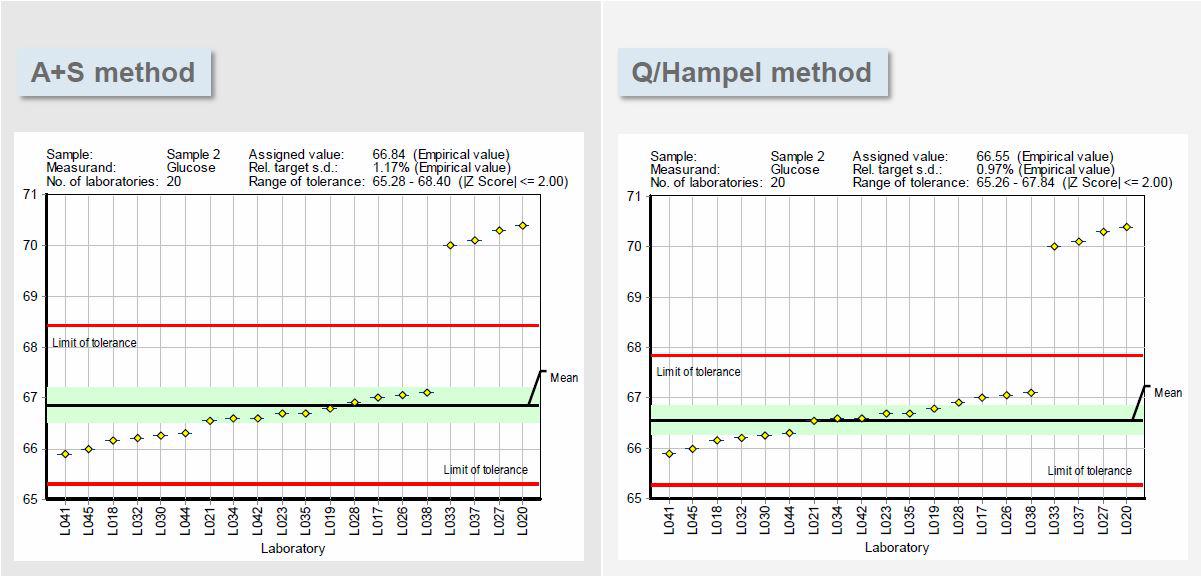
Sehen wir uns an, was passiert, wenn wir ein einziges Laborergebnis ändern:
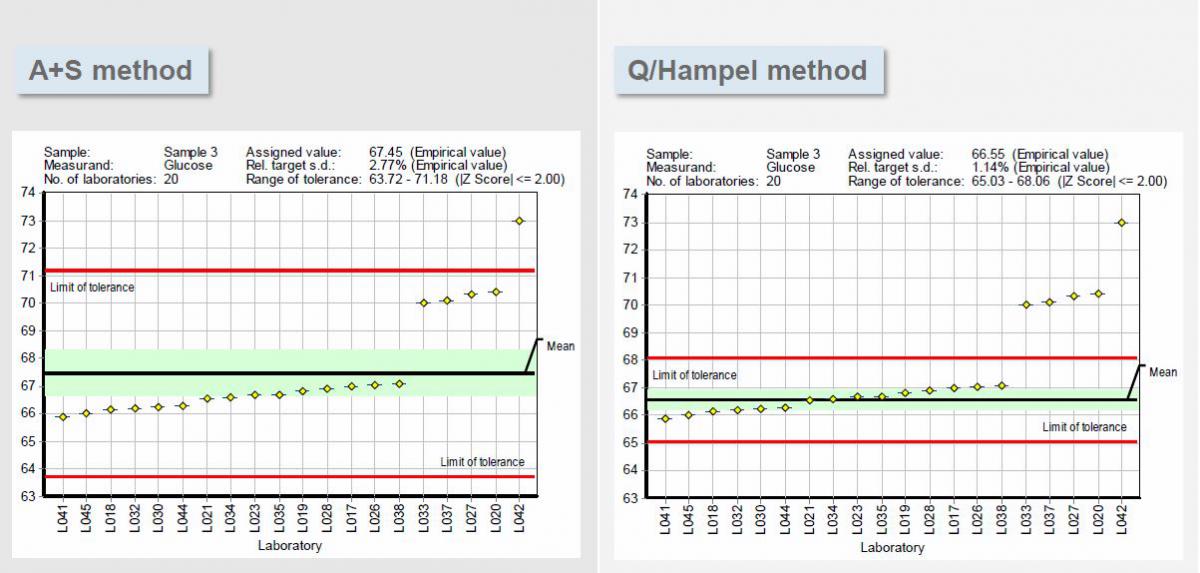
Wie Sie in den folgenden beiden Diagrammen sehen können, ist Labor 42 jetzt auf einem Ast, sein einziger Wert von 73 weicht sogar im Vergleich zu den 4 Ausreißerergebnissen aus dem vorherigen Beispiel weit ab. Beachten Sie, dass im Fall von A+S die vier zuvor bestraften Ausreißer jetzt innerhalb der Toleranzgrenzen liegen. Eine einzige Änderung reicht aus, um die A+S-Berechnungen aus dem Gleichgewicht zu bringen, was zu einer völlig anderen Leistungsbewertung für diese vier Labore führt. Im Fall von Q/Hampel haben sich die Toleranzgrenzen – und der Mittelwert – jedoch kaum verschoben. Die vier zuvor bestraften Labore liegen immer noch außerhalb der Toleranzgrenzen. Q/Hampel hat sich nicht täuschen lassen.
Publikationen zu Q/Hampel
Die Data Scientists von QuoData sind ständig daran interessiert, die Q/Hampel-Methode und andere Standards zu verbessern. Aus diesem Grund veröffentlichen wir eine Vielzahl von Publikationen. Unter anderem:
Steffen Uhlig, Bertrand Colson, Petra Gowik (2018):
Taking laboratory uncertainties into account in the Hampel estimator
In: Accreditation and Quality Assurance
https://link.springer.com/article/10.1007/s00769-018-1332-x
Uhlig, Steffen (2015):
Robust estimation of between and within laboratory standard deviation with measurement results below the detection limit.
In: Journal für Verbraucherschutz und Lebensmittelsicherheit (10), S. 385–391
http://dx.doi.org/10.1007/s00003-015-0967-3
Colson, Bertrand (2014):
The Untold History of Algorithm A.
Hg. v. QuoData GmbH
https://www.quodata.de/en/algorithm-a
